Root Mean Square (RMS) is a fundamental measurement of the magnitude of an AC signal. Its definition is both practical and mathematical. Defined practically, the RMS value assigned to an AC signal is the amount of DC required to produce an equivalent amount of heat in the same load. For example, an AC current of 1 amp RMS will heat a resistor to the same temperature as a 1 amp DC current.
The following is the mathematical definition of the RMS value of a signal:
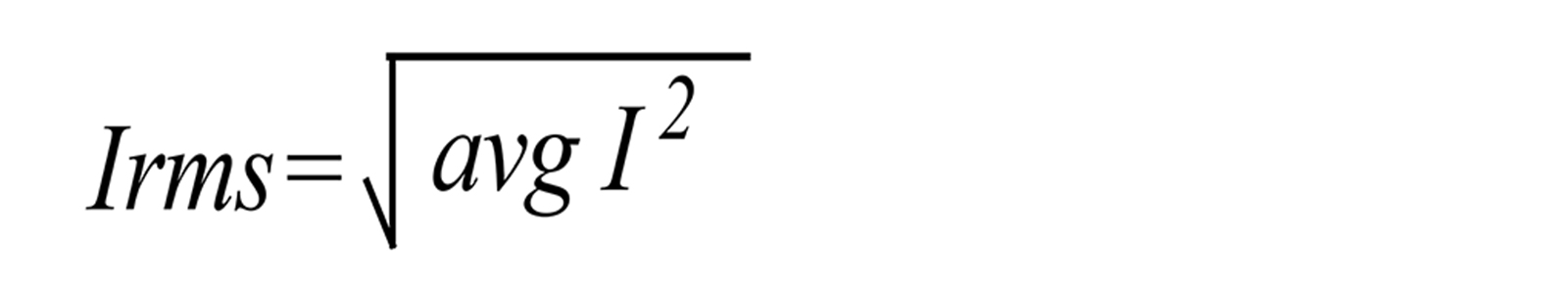
This involves measuring the signal for a time longer than the lowest frequency present, squaring the signal, taking the average value of the square of the signal, and then taking the square root of the signal. In this manner, the true power in the signal is measured.
Another term that arises in RMS measurement is Crest Factor. Crest factor is the ratio of the peak value of a signal to its RMS value. A symmetrical square wave or a DC signal has a crest factor of 1. A pure sine wave has a crest factor of 1.414, and a triangle wave crest factor is 1.73. It can be seen that the more “spiked” a signal is, the higher its crest factor. This is important since the measurement instrument must have a large enough frequency response and dynamic range to capture all features of the signal.
The measurement method of many electronic instruments on the market today is the averaging method. The average value over time is taken as the signal level. This works fine if the AC signal is always the same shape such as a sine wave. Then the reading of the instrument is adjusted such that the value is correct for that wave shape and any further measurements are correct as long as the waveshape does not change.
This measurement is easily implemented by simply using diodes to rectify the AC signal. The problem arises when waveforms occur that are not a known and calibrated. The unknowns may be harmonics, spikes, SCR distortions, or other unknowns. Take, for example, a waveform consisting of a spike that lasts for only about 10% of the cycle time and is zero the rest of the time. The % error for an averaging instrument is about 35% low. For a 5% duty cycle the error is nearly 55% low.
It can be seen that short spikes, such as found in most typical noise and harmonics on AC power lines, are read quite inaccurately by an averaging instrument and the worst of all cases is that they are read low. Thus, anyone dealing with large amounts of power and under measuring this energy will incur serious problems.
True RMS measurement in the Power Industry is becoming increasingly important as the power grid and its large industrial customers become more complex. The complexity of the grid causes increased likelihood of harmonics, particularly odd harmonics, to be present in the system. The complexity of the loads provided by large industrial customers, using large motors, SCR controllers, and rapidly varying power demands, causes substantial spikes, noise, and other transient pulse waveforms to be present on the supply lines.
Utility infrastructure is expensive and customers have a vital dependence on the power that utilities deliver. With today’s available technology, power companies cannot afford to be measuring inaccurately and should maintain their operations with the most accurate equipment available.